Answer:
After 48 months the value will increase by 10 percent of the initial value.
Explanation:
Let's first find the rate of increase for each period which is 3 months here.
According to the table at month
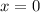 value is
value is
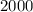 dollars and at month
dollars and at month
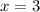 value is
value is
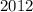 dollars.
dollars.
∴
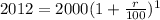
⇒
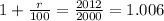
⇒
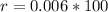
⇒
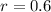 %
%
Now the question is to find how long it will take for the investment value to increase 10 percent.
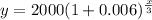
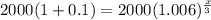
⇒
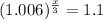
⇒
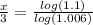
⇒
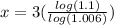
⇒
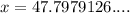
∴at
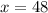 the value will slightly cross 10 percent increase.
the value will slightly cross 10 percent increase.