Answer:
a)
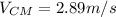
b)
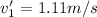
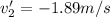
c)
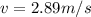
Step-by-step explanation:
The equatiom of velocity of the center mass it is given by:
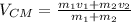
m₁=12 kg, v₁=4 m/s.
m₂=7 kg, v₂=1 m/s.
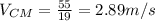
b) The velocity of the first and second particle in the center of mass reference frame is given by:
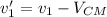 (1)
(1)
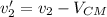 (2)
(2)
So we will have:
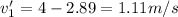
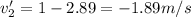
c) Using the conservation of momentum in a perfectly inelastic collision:
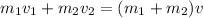 (3)
(3)
Solving (3) for v:
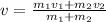 (4)
(4)
Let's recall a perfectly inelastic collision means that the colliding particles stick together afte the collision.
If we see, the equation 4 is the same as the velocity of the center of mass. So v = 2. 89 m/s.
I hope it helps!
Have a nice day!