Question

A processor of carrots cuts the green top off each carrot, washes the carrots, and inserts six to a package. Twenty packages are inserted in a box for shipment. Each box of carrots should weigh 20.4 pounds. The processor knows that the standard deviation of box weight is 0.5 pound. The processor wants to know if the current packing process meets the 20.4 weight standard. How many boxes must the processor sample to be 95% confident that the estimate of the population mean is within 0.2 pound?

Answer 1

24 boxes

Explanation:

The processor knows that the standard deviation of box weight is 0.5 pound

`\sigma = 0.5`

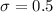
We are supposed to find How many boxes must the processor sample to be 95% confident that the estimate of the population mean is within 0.2 pound

Formula of Error=
`z * (\sigma)/(√(n))`

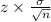
Since we are given that The estimate of the population mean is within 0.2 pound

So,
`z * (\sigma)/(√(n))=0.2`

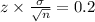
z at 95% confidence level is 1.96

`1.96 * (0.5)/(√(n))=0.2`

`1.96 * (0.5)/(0.2)=√(n)`

`4.9=√(n)`

`(4.9)^2=n`

`24.01=n`

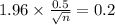
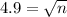
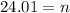
Hence the processor must sample 24 boxes to be 95% confident that the estimate of the population mean is within 0.2 pound