Question

Model rocket engines are sized by thrust, thrust duration, and total impulse, among other characteristics. A size C5 model rocket engine has an average thrust of 5.26 N, a fuel mass of 12.7 g, and an initial mass of 25.5 g. The duration of its burn is 1.90 s. If this engine is placed in a rocket body of mass 54.5 g, and if the rocket is fired in outer space, what is the final velocity of the rocket

Answer 1

v_{f} = 115.95 m / s

Step-by-step explanation:

This is an exercise of a variable mass system, let's form a system formed by the masses of the rocket, the mass of the engines and the masses of the injected gases, in this case the system has a constant mass and can be solved using the conservation the amount of movement. Which can be described by the expressions

Thrust =
`v_(e) (dM)/(dt)`

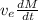
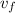`v_(f)`-v₀ = v_{e}
`ln ( (M_(o) )/(M_(f)) )`

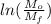
where v_{e} is the velocity of the gases relative to the rocket

let's apply these expressions to our case

the initial mass is the mass of the engines plus the mass of the fuel plus the kill of the rocket, let's work the system in SI units

M₀ = 25.5 +12.7 + 54.5 = 92.7 g = 0.0927 kg

The final mass is the mass of the engines + the mass of the rocket

M_{f} = 25.5 +54.5 = 80 g = 0.080 kg

thrust and duration of ignition are given

thrust = 5.26 N

t = 1.90 s

Let's start by calculating the velocity of the gases relative to the rocket, where we assume that the rate of consumption is linear

thrust = v_{e}
`(M_(f) - M_(o) )/(t_(f) - t_(o) )`

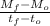
v_{e} = thrust
`(\Delta t)/(\Delta M)`

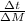
v_{e} = 5.26
`(1.90)/(0.080 -0.0927)`

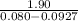
v_{e} = - 786.93 m / s

the negative sign indicates that the direction of the gases is opposite to the direction of the rocket

now we look for the final speed of the rocket, which as part of rest its initial speed is zero

v_{f}-0 = v_{e}
`ln ( (M_(o) )/(M_(f) ) )`

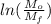
we calculate

v_{f} = 786.93 ln (0.0927 / 0.080)

v_{f} = 115.95 m / s