Answer:
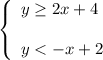
Explanation:
1. The solid line passes trough the points (0,4) and (-2,0). The equation of this line is:

The origin doesn't belong to the shaded region, so its coordinates do not satisfy the inequality. Thus,
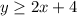
2. The dotted line passes trough the points (0,2) and (2,0). The equation of this line is:
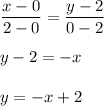
The origin belongs to the shaded region, so its coordinates satisfy the inequality. Thus,
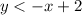
Hence, the system of two inequalities is