Question

I love sharks! In fact, before I became a statistician, I wanted to be a marine biologist specializing in shark research (I even went to school for it for a little while). Of particular interest to me were hammerheads and great whites.

Great white sharks are big and hungry. The lengths of 44 great white sharks tagged near False Bay, South Africa had a mean of 15.6 ft with standard deviation 2.5 feet. Based on this sample, is there evidence that the mean length of great white sharks near False Bay are greater than 15 feet? Use a significance level, α = 0.10.
State the null hypothesis.

Answer 1

Null hypothesis:
`\mu \leq 15`

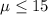
Alternative Hypothesis:
`\mu >15`

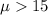
We have enough evidence to reject the null hypothesis at 10% level of significance.

Explanation:

1) Data given

n =44, representing the sample size

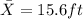`\bar X=15.6ft` represent the sample mean for the length of great white sharks

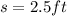`s=2.5ft` represent the sample standard deviation for the length of great white sharks

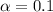`\alpha =0.1` significance level for the test

2) Formulas to use

On this case we are intereste on the sample mean for the length of great white sharks, and based on the paragraph the hypothesis are given by:

Null hypothesis:
`\mu \leq 15`

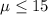
Alternative Hypothesis:
`\mu >15`

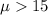
since we have n>30 but we don't know the population deviation
`\sigma` so we will can use the t approximation. The sample mean have the following distribution

`\bar X \sim N(\mu,(\sigma)/(√(n)))`

Based on this the statistic to check the hypothesis would be given by:

`t=(\bar X-\mu)/((s)/(√(n)))`

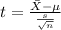
Replacing the values given we have:

`t_(calc)=(15.6-15)/((2.5)/(√(44)))=1.592`

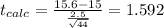
We can calculate the degrees of freedom with:

`df=n-1=44-1=43`

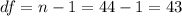
With
`\alpha` and the degrees of freedom we can calculate the critical value, since
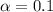`\alpha=0.1` we need a value from the t distribution with 43 degrees of freedom that accumulates 0.1 of the area on the right or 0.9 of the area on the left.

We can use excel, a calculator or a table for this, calculating this value we got:

`t_((43,critc))=1.302`

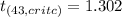
Since our calculatesd value was
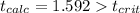`t_(calc)=1.592>t_(crit)`, we can reject the null hypothesis at 0.1 level of significance.

Other way in order to have a criterion for reject or don't reject the null hypothesis is calculating the p value, on this case based on the alternative hypothesis the p value would be given by:

`p_v=P(t_((43))>1.592)=0.0594`

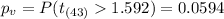
So then
`p_v <\alpha` so we have enough evidence to reject the null hypothesis at 10% level of significance.