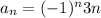Question

-3,6,-9,12,-15 which of the following represents the general term for the sequence give?

(-1)^n3^n
(-1)^n3n
(-1)^n+1(3)

Answer 1

The general term for the sequence
`a_(n)=(-1)^(n) 3 n`

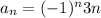
Solution:

Given sequence is -3, 6, -9, 12, -15

We have to find the general term of sequence

The terms in the sequence are found out by using the recursive definition:

`a_(n)=(-1)^(n) 3 n`

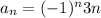
Let us use this definition to find out the terms and check if it matches our given sequence

`\begin{array}{l}{\text { For } n=1:-(-1)^(n) 3 n=(-1)^(1) * 3 * 1=-3} \\\\ {\text { For } n=2:-(-1)^(n) 3 n=(-1)^(2) * 3 * 2=1 * 6=6} \\\\ {\text { For } n=3:-(-1)^(n) 3 n=(-1)^(3) * 3 * 3=-1 * 9=-9} \\\\ {\text { For } n=4:-(-1)^(n) 3 n=(-1)^(4) * 3 * 4=1 * 12=12} \\\\ {\text { For } n=5:-(-1)^(n) 3 n=(-1)^(5) * 3 * 5=-1 * 15=-15}\end{array}`

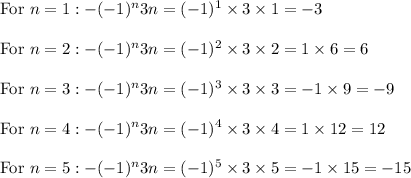
Thus the general term is given by
`a_(n)=(-1)^(n) 3 n`