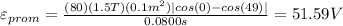Question

A closely wound rectangular coil of 80 turns has dimensions of 25.0 cm by 40.0 cm. The plane of the coil is rotated from a position where it makes an angle of 41.0 ∘ with a magnetic field of 1.50 T to a position perpendicular to the field. The rotation takes 0.0800 s .Part AWhat is the average emf induced in the coil?Express your answer with the appropriate units.

Answer 1

`\varepsilon_(prom)=51.59V`

Step-by-step explanation:

1) Notation and data given

N= 80 represent the turns

B=1.5 T represent the magnetic field

Dimensions =25cm x40cm

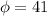`\phi=41`° represent the angle respect to the plpane of the coil

`\phi_i=90-41=49`° since we need the angle respect to the magnetic field

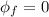`\phi_f =0`° since the final position is perpendicular to the field.

`\Delta t= 0.08s`

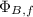`\Phi_(B,f)` represent the final flux through the coil

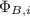`\Phi_(B,i)` represent the initial flux through the coil

`\varepsilon` represent the induced emf, known as "electromagnetic induction" and is defined as "the production of voltage in a coil because of the change in a magnetic flux through a coil" (Variable of interest).

2) Formulas to use

We can begin calculating the area given by:

`A=0.25mx0.40m=0.1m^2`

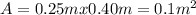
We can use the formula for the average magnitude when we have an induced emf, given by:

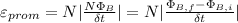`\varepsilon_(prom)=N|(N\Phi_B)/(\delta t)|=N|(\Phi_(B,f)-\Phi_(B,i))/(\delta t)|` (1)

We have another formula for the flux through the coil given by:

`\Phi_B =BAcos(\phi)`

Replacing this into equation (1) we got:

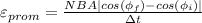`\varepsilon_(prom)=(NBA|cos(\phi_f)-cos(\phi_i)|)/(\Delta t)` (2)

3) Calculate the final answer

Now we can replace all the values given into equation (2) like this:

`\varepsilon_(prom)=((80)(1.5T)(0.1m^2)|cos(0)-cos(49)|)/(0.0800s)=51.59V`