Question

Last year, during an investigation of the time spent reading e-mails on a daily basis, researchers found that on Monday the average time was 50 minutes. Office workers claim that with the increased spam and junk mail, this time has now increased. To conduct a test, a sample of 25 employees is selected with the following results: sample mean = 51.05 minutes and sample standard deviation = 14.2 minutes. What is the critical value for ? = .05 to test the hypotheses. Assume the time spent reading e-mails is normally distributed.

Set up the problem.
Calculate the test statistic.
State your conclusion. Reject/Fail?
Based on your decision about the hypothesis testing what kind error is possible? Type 1 or Type 2

Answer 1

We conclude that with the increased spam and junk mail, the time spent reading e-mails on a daily basis has not increased.

Explanation:

We are given the following in the question:

Population mean, μ = 50 minutes

Sample mean,
`\bar{x}` = 51.05 minutes

Sample size, n = 25

Alpha, α = 0.05

Sample standard deviation, σ = 14.2 minutes

First, we design the null and the alternate hypothesis

`H_(0): \mu = 50\text{ minutes}\\H_A: \mu > 50\text{ minutes}`

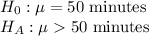
We use One-tailed t test to perform this hypothesis.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(s)/(√(n)) }`

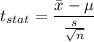
Putting all the values, we have

`t_(stat) = \displaystyle(51.05 - 50)/((14.2)/(√(25)) ) = 0.3697`

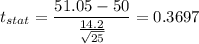
Now,
`t_(critical) \text{ at 0.05 level of significance, 24 degree of freedom } = 1.710882`

Since,

`t_(stat) < t_(critical)`

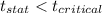
We fail to accept the alternate hypothesis and reject the alternate hypothesis. We accept the null hypothesis. Thus, we conclude that with the increased spam and junk mail, the time spent reading e-mails on a daily basis has not increased.

There maybe a chance to commit type II error, defined as fail to reject the null hypothesis when it is false.