Answer:

Step-by-step explanation:
It is given that,
Mass of object A,
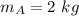
Initial speed of object A,
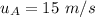
Mass of object B,
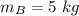
Initial speed of object A,
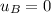 (at rest)
(at rest)
Le V is the final speed when they lock and move with one common velocity. Using the conservation of momentum to find it.
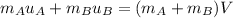
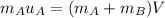
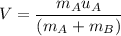
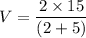
V = 4.28 m/s
Initial kinetic energy of the system is :
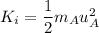
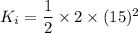
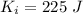
Final kinetic energy of the system is :
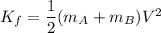
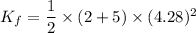
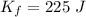

Let
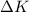 is the change in kinetic energy of the system after the collision. It is given by :
is the change in kinetic energy of the system after the collision. It is given by :
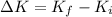
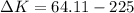

So, the change in kinetic energy of the system is 160.89 Joules.