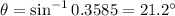Question

Light with a wavelength of 546.1 nm passes through a 6.62 103 lines cm diffraction grating. What is the first-order angle of

diffraction?
a 21.2°
c3920
b. 34.60
d 41.6

Answer 1

The first order angle of diffraction is 21.2°.

Answer: Option A

Step-by-step explanation:

It is known that light waves get diffracted through grating will undergo interference fringes. If the wavelength of light is comparable to the diameter of grating then constructive interference will be formed if and only if the diffracted line obey Bragg’s law i.e.,

`n \lambda = d \sin \theta`

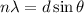
Here d is the grating constant.

`d = (1)/(N)`

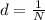
Here N is the number of lines per cm.

Hence,

`N=(1)/(d) = 6.62 * 10^(3) \mathrm{cm}^(-1) = 6.62 * 10^(3) * 10^(2) \mathrm{m}^(-1)`

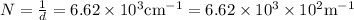
Thus, we get,
`(1)/(d) = 6.62 * 10^(5) \mathrm{m}^(-1)`

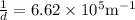
Then the diffraction angle θ can be found as below with n=1 as we need to determine the first order diffraction angle.
`\sin \theta=(n \lambda)/(d)=n \lambda N=1 * 541.6 * 10^(-9) * 6.62 * 10^(5)=3585.4 * 10^(-4)=0.3585`

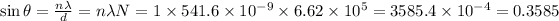
Thus, obtaining the first- order diffraction angle as,

`\theta = \sin ^(-1) 0.3585 = 21.2^(\circ)`