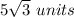Answer:
The height of the equilateral triangle is
Explanation:
we know that
An equilateral triangle has three congruent sides, and three congruent angles that each measure 60 degrees
To find out the height of an equilateral triangle, apply the Pythagoras Theorem in the right triangle ABD
Remember that the height of an equilateral triangle bisects the base.
see the attached figure to better understand the problem
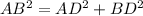
substitute the given values
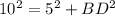
Solve for BD
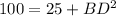
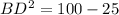
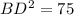

simplify
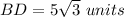 `
`
therefore
The height of the equilateral triangle is