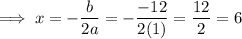Question

What is the line of symmetry for the parabola whose equation is y=x²-12x + 7?

Ox=12
Ox=6
Ox=-6

Answer 1

x = 6

Step-by-step explanation:

The axis of symmetry of a parabola is the x-value of its vertex.

For a quadratic function in the form
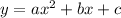`y=ax^2+bx+c`, the x-value of the vertex is:

`x=-(b)/(2a)`

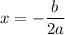
Given function:

`y=x^2-12x+7`

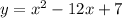
Therefore:

`a=1, \quad b=-12, \quad c=7`

So the axis of symmetry of the given quadratic function is:

`\implies x=-(b)/(2a)=-(-12)/(2(1))=(12)/(2)=6`

Answer 2

x = 6

Step-by-step explanation:

completing square:

`y=x^2-12x+7`

`y=(x^2-12x)+7`

`y=(x-6)^2+7-(-6)^2`

`y=(x-6)^2+7-36`

`y=(x-6)^2-29`

Comparing with quadratic equation
`y=ax^2 + bx+c`, in vertex form where
`y = a(x-h)^2+k`. In this x - h = 0, x = h defines the symmetry of equation.

So here the symmetry for parabola:

x - 6 = 0

x = 6