Answer:
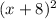 +
+
 =
=

Explanation:
The equation of a circle is given as :
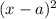 +
+
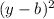 =
=
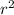
Where (a,b) are the coordinate of the center and r is the radius of the circle.
The end point of the diameter is give as (-5, -3 ) and ( -11 , -3 ) , This means that we can find the coordinate of the center by finding the mid point of the end point. The mid point is calculated by :
Mid point = (
 ,
,
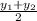 )
)
 = -5
= -5
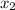 = -11
= -11
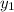 = -3
= -3
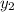 = -3
= -3
Substituting this values into the formula for finding mid point , we have
Mid point = (
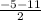 ,
,

Mid-point = (-8 , -3)
Remember that Radius is half of the diameter , To find the diameter we must find the distance between the two end point using the formula for calculating distance between two points , that is
D =
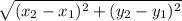
Substituting the values :
D =

D =
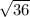
D = 6
Therefore , The diameter i s 6
And since radius is half of the diameter , radius is thus
r = 6/2
r = 3
So , substituting the values gotten into the equation of circle , we have:
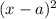 +
+
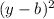 =
=
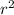
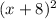 +
+
 =
=
