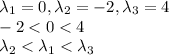Answer:
Characteristic equation:
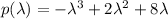
Eigen values:
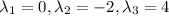
Explanation:
We are given the matrix:
![\displaystyle\left[\begin{array}{ccc}-14&-6&6\\28&12&-4\\0&0&4\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/nwmqmwq70dkkjw8c51h2ofjq269fva1z5q.png)
The characteristic equation can be calculated as:
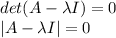
We follow the following steps to calculate characteristic equation:
![=det\Bigg(\displaystyle\left[\begin{array}{ccc}-14&-6&6\\28&12&-4\\0&0&4\end{array}\right]-\lambda\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right]\Bigg)\\\\= det\Bigg(\displaystyle\left[\begin{array}{ccc}-14-\lambda&-6&6\\28&12-\lambda&-4\\0&0&4-\lambda\end{array}\right]\Bigg)\\\\=(-14-\lambda)[(12-\lambda)(4-\lambda)]+6[28(4-\lambda)]-6[(28)(0)-(12-\lambda)(0)]\\\\= -\lambda^3 + 2\lambda^2 + 8\lambda](https://img.qammunity.org/2020/formulas/mathematics/college/2o2ptzfiifof1th6g4apbyxlbczq31fhdi.png)
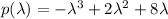
To obtain the eigen values, we equate the characteristic equation to 0:
![p(\lambda) = -\lambda^3 + 2\lambda^2 + 8\lambda = 0\\-\lambda(\lambda^2-2\lambda-8) = 0\\-\lambda(\lambda^2-4\lambda+2\lambda-8) = 0\\-\lambda[(\lambda(\lambda-4)+2(\lambda-4)] = 0\\-\lambda(\lambda+2)(\lambda-4) = 0 \\\lambda_1 = 0, \lambda_2 = -2, \lambda_3= 4](https://img.qammunity.org/2020/formulas/mathematics/college/ibdu9wgt4d2xo0ge8f52sjupb6u4kg8ars.png)
We can arrange the eigen values as: