Answer:
(a) The speed of the target proton after the collision is:
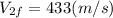 , and (b) the speed of the projectile proton after the collision is:
, and (b) the speed of the projectile proton after the collision is:
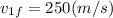 .
.
Step-by-step explanation:
We need to apply at the system the conservation of the linear momentum on both directions x and y, and we get for the x axle:
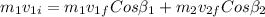 , and y axle:
, and y axle:
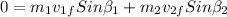 . Now replacing the value given as:
. Now replacing the value given as:
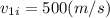 ,
,
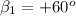 for the projectile proton and according to the problem
for the projectile proton and according to the problem
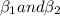 are perpendicular so
are perpendicular so
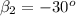 , and assuming that
, and assuming that
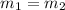 , we get for x axle:
, we get for x axle:
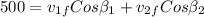 and y axle:
and y axle:
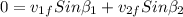 , then solving for
, then solving for
 , we get:
, we get:
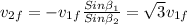 and replacing at the first equation we get:
and replacing at the first equation we get:
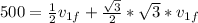 , now solving for
, now solving for
 , we can find the speed of the projectile proton after the collision as:
, we can find the speed of the projectile proton after the collision as:
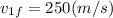 and
and
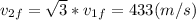 , that is the speed of the target proton after the collision.
, that is the speed of the target proton after the collision.