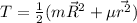Question

verify that the positions of two particles can be written in terms of CM the CM and relative positions as r1 = R + m2r/M and r2 = R − m1r/M. Hence confirm that the total KE of the two particles can be expressed as T = 1 2MR˙ 2 + 1 2 µr˙ 2 , where µ denotes the reduced mass µ = m1m2/M.

Answer 1

To solve the problem it is necessary to resort to the concepts of kinetic energy of the bodies.

Kinetic energy in vector form can be expressed as

`KE = (1)/(2)m\vec{R}^2`

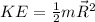
According to the description given we have to

`r_1 = R+ m_2r/M`

`r_2 = R-m_1 r/M`

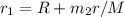
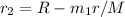
Equating both equation we have that

`R = (m_1r_1+m_2r_2)/(m_1+m_2)`

`R = (m_1r_1+m_2r_2)/(M)`

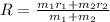
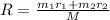
The kinetic energy of the two particles would be given by

`T = (1)/(2) (m_1\vec{r_1}^2+m_2\vec{r_2}^2)`

`T = (1)/(2) (m_1(\vec{R}+(m_2)/(M)\vec{r})^2+m_2(\vec{R}-(m_1)/(M)\vec{r})^2)`

`T = (1)/(2) (m\vec{R}^2+(m_1m_2)/(M)\vec{r}^2)`

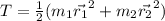
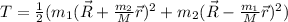
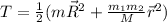
We have the consideration that

`\mu = (m_1m_2)/(M)`

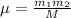
Then replacing,

`T = (1)/(2)(m\vec{R}^2+\mu\vec{r^2})`