Question

Consider the graph of the line y = -x-4 and the point

(-4,2).
The slope of a line parallel to the given line is
A point on the line parallel to the given line, passing
through (-4,2), is
The slope of a line perpendicular to the given line is
A point on the line perpendicular to the given line
passing through (-4, 2), is

Answer 1

1/2

(0,4)

-2

(-2,-2)

Explanation:

edge

Answer 2

-1

y = -x -2

1

y = x + 6

Explanation:

Given line is y = - x - 4

We know that the equation of a line is of the form y = mx + c where m is the slope of the line and c is a constant

Now The slope of the given line is m = -1

We know that the slope of any line parallel to the given line is same the original one

Therefore the slope of the line parallel to the given line is -1

Given the point is ( -4 , 2 ) and slope is -1

We know that the equation of a line passing through the point (c , d) and slope m is

`y - d=m*(x-c)`

Here the equation is

`y-2=-1*(x-(-4))`

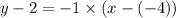
y = -x -2

We know that if two lines with slopes m1 and m2 are perpendicular then m1m2 = -1

Here m1 = -1 then

m2 = 1

Given the point is ( -4 , 2 ) and slope is 1

We know that the equation of a line passing through the point (c , d) and slope m is

`y - d=m*(x-c)`

Here the equation is

`y-2=1*(x-(-4))`

y = x + 6