Question

​Find all roots: x^3 + 7x^2 + 12x = 0
Show all work and check your answer.

Answer 1

The three roots of x^3 + 7x^2 + 12x = 0 is 0,-3 and -4

Solution:

We have been given a cubic polynomial.

`x^(3)+7 x^(2)+12 x=0`

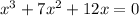
We need to find the three roots of the given polynomial.

Since it is a cubic polynomial, we can start by taking ‘x’ common from the equation.

This gives us:

`x^(3)+7 x^(2)+12 x=0`

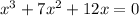
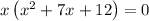`x\left(x^(2)+7 x+12\right)=0` ----- eqn 1

So, from the above eq1 we can find the first root of the polynomial, which will be:

x = 0

Now, we need to find the remaining two roots which are taken from the remaining part of the equation which is:

`x^(2)+7 x+12=0`

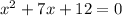
we have to use the quadratic equation to solve this polynomial. The quadratic formula is:

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

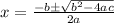
Now, a = 1, b = 7 and c = 12

By substituting the values of a,b and c in the quadratic equation we get;

`\begin{array}{l}{x=\frac{-7 \pm \sqrt{7^(2)-4 * 1 * 12}}{2 * 1}} \\\\{x=(-7 \pm √(1))/(2)}\end{array}`

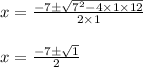
Therefore, the two roots are:

`\begin{array}{l}{x=(-7+√(1))/(2)=(-7+1)/(2)=(-6)/(2)} \\\\ {x=-3}\end{array}`

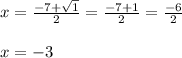
And,

`\begin{array}{c}{x=(-7-√(1))/(2)} \\\\ {x=-4}\end{array}`

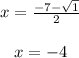
Hence, the three roots of the given cubic polynomial is 0, -3 and -4