Question

You deposit a thin film of magnesium difluoride on a glass lens (n >1.60), reducing the reflection of yellow light, at normal incidence, to a minimum. You find that the thinnest coating that accomplishes this is 106 nm thick. The index of refraction for MgF2 for yellow light (λ = 585 nm) is

A. 1.50.
B. 1.38.
C. 1.15
D. 1.00.
E. 0.707.

Answer 1

To solve this problem it is necessary to apply the concepts related to destructive interference.

The concept refers to an overlap of two or more waves of identical or similar frequency that, when interfering, creates a new pattern of waves of lower intensity

By definition destructive interference is given by

`2Mt = (n+(1)/(2))\lambda`

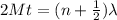
Where,

`\lambda= wavelength`

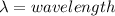
n=integer (1,2,3,4,5,6...etc)

t = thickness

M= Index of refrqaction

For minimum thickness to satisfy this condition n will be minimum there,

n=0

Therefore

`2Mt = (0+(1)/(2))\lambda`

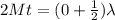
Solving to find M,

`M = (\lambda)/(4t)`

`M = (585nm)/(4*106nm)`

`M = 1.38`

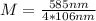
Therefore the correct answer is B. 1.38