Question

An object is accelerates for 10 seconds at 8 m/s after a force of 300 joules is applied to it. . What is the mass?

Answer 1

37.5

Step-by-step explanation:

m = F ÷ a; F ÷ a = m

300 ÷ 8 = 37.5

Hope this helps,

♥A.W.E.S.W.A.N.♥

Answer 2

The mass of the object for the given problem is 9.375 kg

Step-by-step explanation:

As the force is given in terms of energy, this means the work done on the object to move it has been given as 300 J. As the work done on any system is equal to the variations in the object's kinetic energy.

As the object's kinetic energy at rest will be zero due to zero initial velocity, the work done will be equal to the final kinetic energy of the object in moving after application of this force. It is known that kinetic energy is the energy required by the object to be in motion.

Also it is known that the kinetic energy required to move an object will be directly proportionate to the product of mass of the object and the velocity attained by the object. Thus,

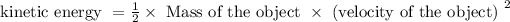
`\text { kinetic energy }=(1)/(2) * \text { Mass of the object } * \text { (velocity of the object) }^(2)`

So,

`\text { Mass of the object }=\frac{2 * \text { Kinetic energy }}{\text { (velocity of the object) }^(2)}`

`\text { Mass of the object }=\frac{2 * 300 \mathrm{J}}{8 * 8 \mathrm{m}^(2) \mathrm{s}^(-2)}=\frac{600 \mathrm{kgm}^(2) \mathrm{s}^(-2)}{64 \mathrm{m}^(2) \mathrm{s}^(-2)}=9.375 \mathrm{kg}`

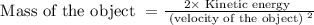
Thus, the mass of the object is 9.375 kg.