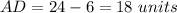Question

Use the diagram, which is not drawn to scale to find AD if you know that AC=24 & BC=12

a.6
b.18
c.16.97
d.20.78

Answer 1

B. 18

Explanation:

Answer 2

Option b.
`AD=18\ units`

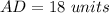
Explanation:

step 1

In the right triangle ABC

Find the sine of angle CAB

`sin(<CAB)=(BC)/(AC)` ---> the sine of angle CAB is equal to divide the opposite side angle CAB (BC) by the hypotenuse (AC)

substitute

`sin(<CAB)=(12)/(24)`

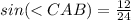
simplify

`sin(<CAB)=(1)/(2)` ---->equation A

step 2

In the right triangle BDC

Find the sine of angle CBD

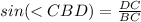`sin(<CBD)=(DC)/(BC)` ---> the sine of angle CBD is equal to divide the opposite side angle CBD (DC) by the hypotenuse (BC)

substitute

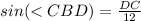`sin(<CBD)=(DC)/(12)` ----> equation B

step 3

we know that

If two figures are similar, then the ratio of its corresponding sides is proportional and its corresponding angles are congruent

In this problem

Triangles ABC and BDC are similar by AA Similarity Theorem

therefore

m∠CBD≅m∠CAB

equate equation A and equation B

`(DC)/(12)=(1)/(2)`

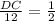
solve for DC

`DC=(12)/(2)=6\ units`

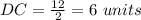
step 4

Find the value of AD

`AD=AC-DC`

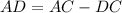
substitute the values

`AD=24-6=18\ units`