Dwight's salary after t year is represented by
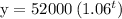
Solution:
Given that
Dwight has a new job that guarantees a six percent raise for each year with the company.
His initial salary is $52,000 per year.
Need to determine equation which models Dwight's salary after t years
Dwight's initial salary = $52,000 per year.
As job guarantees a six percent raise for each year
Dwight's salary after 1 year = 52000 + 6% of 52000 = 52000 + 0.06 x 52000 = 52000 (1.06)
Dwight's salary after 2 year = (52000 x 1.06) + 6 % of (52000 x 1.06)
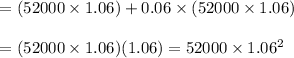
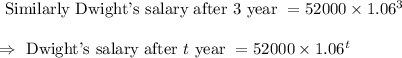
Hence Dwight's salary after t year is represented by =
