Answer:
Length of the training track running around the field
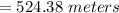
Explanation:
Length of the training track = Outer boundary measures Or Circumference of the field.
We have a rectangular enclosure and circumference/perimeter of a rectangle
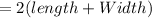
And we have
 semicircle of same measures,
semicircle of same measures,
 semicircles of same measure can be considered as a full circle.
semicircles of same measure can be considered as a full circle.
So circumference of a circle
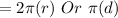 where
where
 is the radius and
is the radius and
 is the diameter.
is the diameter.
And we see we have already being given the values of length ,width but nowhere it has mentioned the diameter.
But from the figure if we look upon,the width of the rectangle is the diameter of the semicircle,so diameter of the circle which is

Finally the training track length = Perimeter of rectangle + Circumference of the circle,which

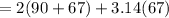
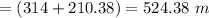
So the length of the training track
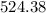 in meters.
in meters.
The units are in meters.