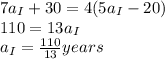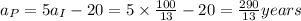Answer:
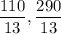
Explanation:
Let
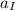 be the present age of I.
be the present age of I.
Let
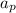 be the present age of P.
be the present age of P.
 years ago P was
years ago P was
 times older than l.
times older than l.
Age of P
 years ago is
years ago is
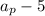
Age of I
 years ago is
years ago is
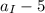
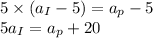 ....(i)
....(i)
After
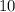 years l will be
years l will be
 as old as P.
as old as P.
Age of P
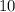 years after is
years after is
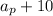
Age of I
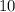 years after is
years after is

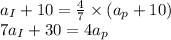 ...(ii)
...(ii)
using (i) and (ii),