Answer:
x = 0.1116 (rounded to 4 decimal places)
Explanation:
We need to isolate "e" first, so we do:
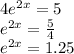
Solving these types of equations requires us to take the Natural Logarith (Ln) of both sides, so we have:
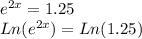
We can use the property of logarithms shown below to further simplify:
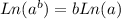
So, we have:
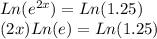
We know Ln(e) = 1, thus now, we can replace it and solve for x:
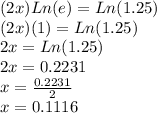
So
x = 0.1116 (rounded to 4 decimal places)