Question

A merchant bought some shirts for $120. The next day the price charged for each shirt was reduced by $1. The merchant calculated that, at the sale price, he could have bought 10 more shirts for $120. How many shirts did he buy originally?

Answer 1

30 shirts

Explanation:

Let x be the number of shirts a mercant bought initially.

He bought them for $120, so each shirt costed
`(\$120)/(x)`

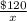
The next day the price charged for each shirt was reduced by $1, so the new price of the shirt became

`(\$120)/(x)-\$1`

The merchant calculated that, at the sale price, he could have bought 10 more shirts, so he could buy x + 10 shirts.

Number of shirts = x + 10

Price of each shirt
`=(\$120)/(x)-\$1`

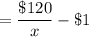
Total cost = $120

Hence,

`(x+10)\left((120)/(x)-1\right)=120\\ \\(x+10)(120-x)=120x\\ \\120x-x^2+1,200-10x=120x\\ \\-x^2-10x+1,200=0\\ \\x^2+10x-1,200=0\\ \\D=10^2-4\cdot (-1,200)=100+4,800=4,900\\ \\x_(1,2)=(-10\pm √(4,900))/(2)=-40,\ 30.`

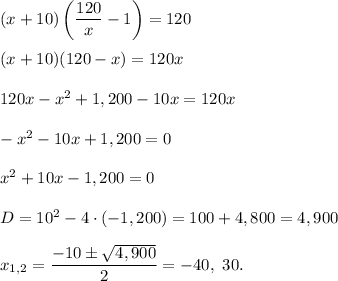
The number of shirts cannot be negative, so x = 30.