Question

A company claims that less than 10% of adults own a smart watch. You want to test this claim, and you find that in a random sample of 100 adults, 12% say that they own a smart watch. Calculate the appropriate standardized test statistic (round to three decimal places). If the conditions are not met (e.g., np < 5), then write "NA." Flag this Question Question 192 pts In the previous question about smart watches, what is the appropriate critical value (to two decimal places), if you wish to conduct the test at alpha = 0.01?

Answer 1

Test statistic is 0.67

Critical value is -2.33

Explanation:

Consider the provided information.

The formula for testing a proportion is based on the z statistic.

`z=\frac{\hat p-p_0}{\sqrt{p_0(1-p_0)/(n)}}`

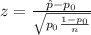
Were
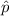`\hat p` is sample proportion.

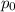`p_0` hypothesized proportion and n is the smaple space,

Random sample of 100 adults, 12% say that they own a smart watch.

A company claims that less than 10% of adults own a smart watch.

Therefore, n = 100
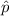`\hat p` = 0.12 ,
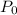`P_0` = 0.10

`1 - P_0 = 1 - 0.10 = 0.90`

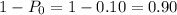
Substitute the respective values in the above formula.

`z=\frac{0.12-0.10}{\sqrt{0.10(0.90)/(100)}}`

`z\approx 0.67`

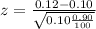
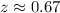
Hence, test statistic = 0.67

This is the left tailed test.

Now using the table the P value is:

P(z < 0.667) = 0.7476

P-value = 0.7476

`\alpha = 0.01`

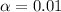
Here, P-value > α therefore, we are fail to reject the null hypothesis.

`Z_(\alpha)= Z_(0.01) = -2.33`

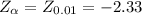
Hence, Critical value is -2.33