Answer:
The total number of ticket booked altogether for students and adults is 126.
Explanation:
The ratio of Number of senior tickets sold: Number of adult tickets = 2:3.
or, Se : A = 2 : 3 ......... (1)
The ratio of Number of adult tickets : Number of student tickets = 6:15
or, A : St : 6 : 15 ........ (2)
Part - A : Given: Senior ticket sold = 24
Now, Let us assume the number of adult tickets sold = m
So Number of Senior tickets : Adult tickets = 24 : m .......... (3)
Comparing (1) and (3)
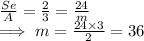
Hence, the number of adult tickets booked is m = 36 tickets
Part - B
Adult tickets booked = 36 (From A)
Now, Let us assume the number of students tickets sold = n
So Number of Adult tickets : students tickets = 36 : n .......... (4)
Comparing (2) and (4)
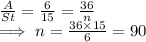
Hence, the number of students tickets booked is n = 90 tickets
⇒ The number of adult tickets booked is 36 tickets
⇒Number of students tickets booked is 90 tickets
Hence, the total number of ticket booked altogether for students and adults is 90 + 36 =126.