Question

What is the slope of the given line segment?

What is the midpoint of the given line segment?
What is the slope of the perpendicular bisector off the given line segment?
What is the equation, in the slope-interception form, of the perpendicular bisector?

Answer 1

Part 1) The slope of the given line segment is
`m=-2`

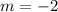
Part 2) The midpoint of the given line segment is (2,-2)

Part 3) The slope of the perpendicular bisector of the given line segment is
`m_2=(1)/(2)`

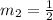
Part 4) The equation, in the slope-interception form, of the perpendicular bisector is
`y=(1)/(2)x-3`

Explanation:

Part 1) What is the slope of the given line segment?

we know that

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

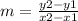
we have the points

(4,-6) and (0,2)

substitute in the formula

`m=(2+6)/(0-4)`

`m=(8)/(-4)=-2`

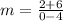
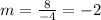
Part 2) What is the midpoint of the given line segment?

We know that

The formula to calculate the midpoint between two points is equal to

`M((x1+x2)/(2),(y1+y2)/(2))`

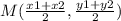
we have the points

(4,-6) and (0,2)

substitute in the formula

`M((4+0)/(2),(-6+2)/(2))`

`M(2,-2)`

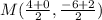
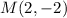
Part 3) What is the slope of the perpendicular bisector of the given line segment?

we know that

If two lines are perpendicular, then their slopes are opposite reciprocal (the product of their slopes is equal to -1)

`m_1*m_2=-1`

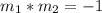
we have

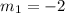`m_1=-2` ---> slope of the given line segment

substitute

`(-2)*m_2=-1`

`m_2=(1)/(2)`

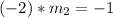
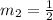
Part 4) What is the equation, in the slope-interception form, of the perpendicular bisector?

The equation of the line in slope intercept form is equal to

`y=mx+b`

we have

`m=(1)/(2)`

The perpendicular bisector passes through the midpoint of the given line segment

`M(2,-2)`

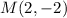
substitute

`-2=(1)/(2)(2)+b`

`-2=1+b`

`b=-3`

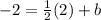
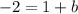
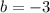
therefore

`y=(1)/(2)x-3`