Answer:
The Time period for investment at 6 % semiannually is 27 years
Explanation:
Given as :
The principal investment = $ 1000
The rate of interest = 6% compounded semiannually
The Amount after T year = $ 1350
Let the time period = T year
Now, From compounded method
Amount = Principal ×
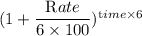
or, $ 1350 = $1000 ×
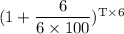
Or,
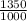 =
=
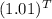
Or, 1.35 =
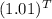
or,
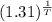 = 1.01
= 1.01
Now Taking log both side
Log
/(T)](https://img.qammunity.org/2020/formulas/mathematics/high-school/l4nphntvii7l8q8cvafqn60agp60xqtjj2.png) × 0.11727 = 0.0043213
× 0.11727 = 0.0043213
So, T =
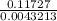
∴ T = 27.11 ≈ 27 years
Hence The Time period for investment at 6 % semiannually is 27 years . Answer