Question

Based on the Nielsen ratings, the local CBS affiliate claims its 11:00 PM newscast reaches 41 % of the viewing audience in the area. In a survey of 100 viewers, 36% indicated that they watch the late evening news on this local CBS station.

30. What is the null hypothesis?
31. What is the alternate hypothesis?
32. What is the sample proportion?
33. What is the critical value if a = 0.01 ?
34. What is the z-statistic?
35. What is the critical value if the level of significance is 0.10?
36. What is your decision if a = 0.01

Answer 1

null hypothesis is p=0.41

alternate hypothesis is p<0.41

Sample proportion is 0.36

critical value for a = 0.01 is -2.2326

z-statistic is −1,0166

critical value for the level of significance 0.10 is -1.28155

we fail to reject the null hypothesis in 0.01 significance level.

Explanation:

Let p be the proportion of the viewing audience of 11:00PM CBS newscast in the area. Then

`H_(0)`: p=0.41

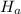`H_(a)`: p<0.41

Sample proportion is 0.36 and critical value (left tailed) for a=0.01 is -2.2326

sample proportion Z-score can be calculated as follows:

z(0.36)=
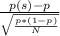`\frac{p(s)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(s) is the sample proportion of vieved newscast (0.36)

• p is the proportion assumed under null hypothesis. (0.41)

• N is the sample size (100)

putting the numbers z(0.36)=
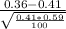`\frac{0.36-0.41}{\sqrt{(0.41*0.59)/(100) } }` =−1,0166

if the level of significance is 0.10 then critical value would be -1.28155.

in 0.01 significance level sample mean is not in the critical region, therefore we fail to reject the null hypothesis.