Answer: It will reject the null hypothesis.
Explanation:
Since we have given that
Hypothesis:
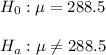
n = 24
Average mean = 289.7 grams
Standard deviation = 5.6 grams
We need to find the 95% confidence interval.
Since n = 24 <30 , so we will use t test.
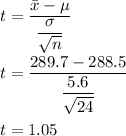
Now, degrees of freedom = n- 1 = 24-1 =23
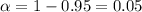
So,
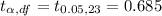
Since t(calculated)>t
1.05>0.685
So, it will reject the null hypothesis.