Question

Seven pieces of rope have an average (arithmetic mean) length of 68 centimeters and a median length of 84 centimeters. If the length of the longest piece of rope is 14 centimeters more than 4 times the length of the shortest piece of rope, what is the maximum possible length, in centimeters, of the longest piece of rope?

Answer 1

The maximum possible length, in centimeters, of the longest piece of rope is 134 cm

Explanation:

Let the seven pieces be a,b,c,d,e,f,g

Average of 7 pieces of ropes =68

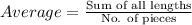
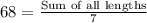
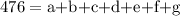`Average = \frac{\text{Sum of all lengths}}{\text{No. of pieces}}`

`68= \frac{\text{Sum of all lengths}}{7}`

`68 * 7 =\text{a+b+c+d+e+f+g}`

`476=\text{a+b+c+d+e+f+g}` --A

We are given that the median length of a piece of rope is 84 centimeters.

We arrange the pieces in the ascending order

So, median will be the length of 4th piece

So, d = 84 cm

the length of piece a,b,c will be less than 84 and the value of e,f,g must be greater than or equal to 84

Let us suppose the length of a,b,c be x

Let us suppose the length of e,f be 84

The length of the longest piece of rope is 14 centimeters more than 4 times the length of the shortest piece of rope

So, g = 4x+14

Substitute the value in A

`476=x+x+x+84+84+84+4x+14`

`476=7x+266`

`(476-266)/(7)=x`

`30=x`

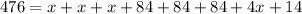
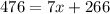
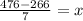
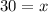
g = 4x+14=4(30)+14=134

Hence the maximum possible length, in centimeters, of the longest piece of rope is 134 cm