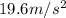To solve this problem it is necessary to apply the concepts related to energy conservation as well as centripetal acceleration.
By conserving energy we know that
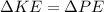
Where,
KE = Kinetic Energy
PE = Potential Energy
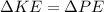
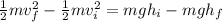
Initial Kinetic Energy according the statement is zero, same as final potential energí, therefore
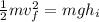
Re-arrange for v,

Where h here represent the radius of hemispherical bowl.
We have also the definition of centripetal acceleration, which is
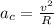
But we have that the radius is equal to the height, then
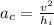
Replacing the previous value of velocity found,
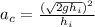
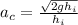
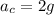
Substituting the value for gravitational acceleration
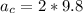
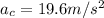
Therefore the radial acceleration of ice cube at bottom is