Question

Points B, D, and F are midpoints if the sides of ACE. EC=38 and DF=16. Find AC

Please show all steps

Answer 1

AC=32 units.

Step by step explanation:

Given information: B, D, and F are midpoints if the sides of ΔACE, EC = 38 and DF = 16.

Consider the below figure attached with this question.

According to the midpoint theorem, if a line segments connecting two midpoints then the line is parallel to the third side and it's length is half of the third side.

Since F and D are midpoints of AE and EC respectively.

Using midpoint theorem, the length of AC is twice of DF.

`AC=2* DF`

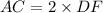
Substitute the given values in the above equation.

`AC=2* 16`

`AC=32`

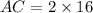
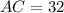
Therefore, the length of AC is 32 units.