Answer:
(a) Bacterial 1 had a faster rate of growth.
(b) The population of f(x) always exceed the population of g(x). In other words, population of g(x) cannot exceed the population of f(x).
Explanation:
Consider the given functions are
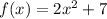
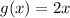
where, x is the time (in hours) and f(x) and g(x) are the number of bacteria (in thousands).
(a)
The rate of change of a function f(x) on [a,b] is
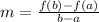
Rate of change between third and sixth hour of first function is
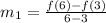
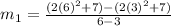
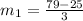

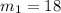
Rate of change between third and sixth hour of second function is
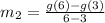
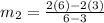
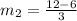
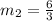

Since
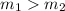 , therefore bacterial 1 had a faster rate of growth.
, therefore bacterial 1 had a faster rate of growth.
(b)
The initial population of f(x) is 7 and it increases exponentially.
The initial population of g(x) is 0 and it increases linearly.
It means population of f(x) always exceed the population of g(x).
In other words, population of g(x) cannot exceed the population of f(x).