Question

A heat engine accepts 200,000 Btu of heat from a source at 1500 R and rejects 100,000 Btu of heat to a sink at 600 R. Calculate the entropy change of all the components of this engine and determine if it is completely reversible. How much total work does it produce?

Answer 1

To solve the problem it is necessary to apply the concepts related to the conservation of energy through the heat transferred and the work done, as well as through the calculation of entropy due to heat and temperatra.

By definition we know that the change in entropy is given by

`\Delta S = (Q)/(T)`

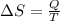
Where,

Q = Heat transfer

T = Temperature

On the other hand we know that by conserving energy the work done in a system is equal to the change in heat transferred, that is

`W = Q_(source)-Q_(sink)`

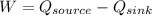
According to the data given we have to,

`Q_(source) = 200000Btu`

`T_(source) = 1500R`

`Q_(sink) = 100000Btu`

`T_(sink) = 600R`

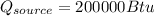
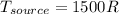
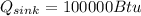
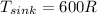
PART A) The total change in entropy, would be given by the changes that exist in the source and sink, that is

`\Delta S_(sink) = (Q_(sink))/(T_(sink))`

`\Delta S_(sink) = (100000)/(600)`

`\Delta S_(sink) = 166.67Btu/R`

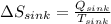
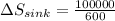
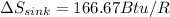
On the other hand,

`\Delta S_(source) = (Q_(source))/(T_(source))`

`\Delta S_(source) = (-200000)/(1500)`

`\Delta S_(source) = -133.33Btu/R`

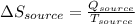
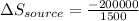
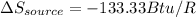
The total change of entropy would be,

`S = \Delta S_(source)+\Delta S_(sink)`

`S = -133.33+166.67`

`S = 33.34Btu/R`

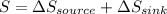
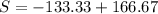
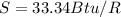
Since
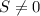`S\\eq   0` the heat engine is not reversible.

PART B)

Work done by heat engine is given by

`W=Q_(source)-Q_(sink)`

`W = 200000-100000`

`W = 100000 Btu`

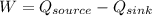
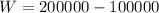
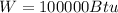
Therefore the work in the system is 100000Btu