Step-by-step explanation:
The centripetal force acting on a particle is given by :
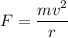
Since,
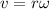
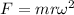
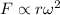
Case 1.
If
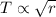
Since,
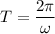
So,
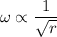
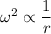
So, the force becomes,
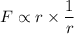
F is independent of r
Case 2.
If
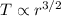
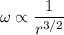
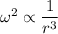
So,
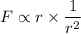
So, the force is inversely proportional to the square of radius.
Case 3.
If T is independent of r, the force will be directly proportional to the radius of orbit.
Hence, this is the required solution.