Answer:
10 square inches.
Explanation:
The area
 of a trapezoidal package with bigger base
of a trapezoidal package with bigger base
 , height
, height
 , and smaller base
, and smaller base
 , is
, is
 .
.
In our case


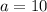
therefore we have
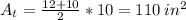
the area of the trapezoid is 110 square inches.
Now, the area
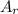 of the rectangular package is its length times height
of the rectangular package is its length times height
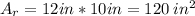
the area of the rectangle is 120 square inches.
The difference in area between the two packages is
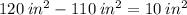
10 square inches.