Question

2. The half-life of the radioactive material in Z-Med, a medication used for certain types of therapy, is 2 days. A patient receives a 16 mCi dose (millicuries,

a measure of radiation) in his treatment. (Half-life means that the radioactive material decays to the point where only half is left.)
a. Make a table to show the level of Z-Med in the patient’s body after nn days
b. Write a formula to model the half-life of Z-Med for nn days. (Be careful here. Make sure that the formula
works for both odd and even numbers of days.)
c. How much radioactive material from Z-Med is left in the patient’s body after 20 days of receiving the
medicine?

Answer 1

Answer: a. The table below shows the level of Z- Med in the patient's body

nn y = f(nn)

0 16

2 8

4 4

6 2

7 1

8 0.5

10 0.25

14 0.125

16 0.0625

18 0.03125

20 0.015625

… …

nn f(nn -1)/2

b. The formula to model the half-life of Z-Med for nn days is given by

`y = f(nn) = 16(0.7071)^(nn)`

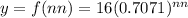
c. The radioactive material from Z-Med is left in the patient’s body after 20 days of receiving the medicine is 0.0156 mCi (4 d.p)

Explanation:

a. To make the table one has to have a left hand column with nn, which represents the number of days and a right hand column with y, which represents the residual radioactive material as per that number of days. It should be noted that the table has an interval of two days because that is the half-life of the drug. And the residual drug reduces by half the quantity from the previous interval.

b. To get the formula for the model, one has to understand that this is an exponential type model which has the general form of
`y=ab^(x)`.

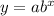So, to get this formula we should take two intervals from the table, preferably (0,16) and (2,8)

`16 = ab^(0)` Therefore, a = 16

`8 = 16* b^(2)`

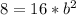
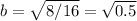`b = √(8/16)  = √(0.5)` Therefore, b = 0.7071

Now applying these constants to the formula we are trying to derive

`y = f(nn) = 16(0.7071)^(nn)`

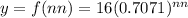
c. To find the quantity of radioactive material left in the patient's body after 20 days just substitute nn with 20

`y = 16(0.7071)^(20)`

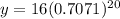
y = 0.015622003

y = 0.0156 mCi (4 d.p)