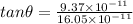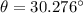Answer:
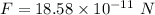
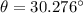
Step-by-step explanation:
Given:
mass of first particle,
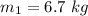
mass of second particle,
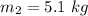
mass of third particle,
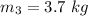
coordinate position of first particle in meters,
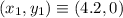
coordinate position of second particle in meters,
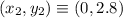
coordinate position of third particle in meters,
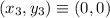
Now, gravitational force on particle 3 due to particle 1:
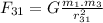
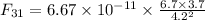
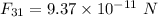
towards positive Y axis.
gravitational force on particle 3 due to particle 2:
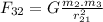

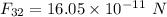
towards positive X axis.
Now the net force

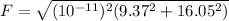
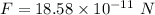
For angle in counterclockwise direction from the +x-axis