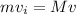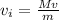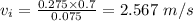Question

A 75 gram ball is fired into a 200 gram pendulum and the center of gravity of the pendulum-ball rises to a height of 2.5 cm. The length from the pivot point to the center of gravity of the pendulum-ball is 30cm. Determine the initial velocity of the ball.

Answer 1

The initial velocity of the ball is 2.567 m/s

Solution:

Mass of the ball, m = 75 gm = 0.075 kg

Mass of the pendulum, m' = 200 gm = 0.2 kg

Height of rise of the ball, h = 2.5 cm = 0.025 m

Length, l = 30 cm = 0.3 m

Now,

Total mass, M = m + m' = 0.075 + 0.2 = 0.275 kg

Now,

Suppose the initial velocity of the ball be
`v_(i)`

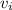
The total mass is raised to a height of 0.025 m after the ball has been fired, thus the total potential energy of the system is given by:

`PE = Mgh = 0.275* 9.8* 0.025 = 0.0674\ J`

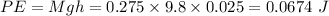
Now, the initial kinetic energy of the system:

`KE = (1)/(2)Mv^(2)`

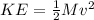
Now, using law of conservation of energy:

PE = KE

`(1)/(2)Mv^(2) = 0.0674`

`v = \sqrt{(0.13475)/(0.275)} = 0.7\ m/s`

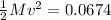
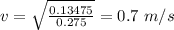
Now by using the principle of momentum conservation:

`mv_(i) = Mv`

`v_(i) = (Mv)/(m)`

`v_(i) = (0.275* 0.7)/(0.075) = 2.567\ m/s`