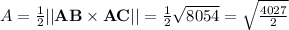Answer:
The area of the triangle is
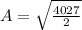
Explanation:
Using the fact that the area of the triangle having u and v as adjacent sides is given by
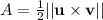
We know that we want to take a cross product to compute the area of the triangle, but we need to be careful because it doesn't make sense if we take the cross product of points.
The first step is to build some vectors that describe this triangle.
According with the graph we can build the vectors:
 and
and
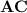
The vector
 is the difference of point B minus point A
is the difference of point B minus point A

and the vector
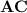 is the difference of point C minus point A
is the difference of point C minus point A
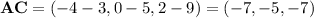
Next we need to find the cross product of this vectors.

This is the definition of cross product of two vectors in space:
Let
 and
and
 be vectors in space. The cross product of
be vectors in space. The cross product of
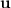 and
and
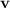 is the vector
is the vector
Applying this definition we get

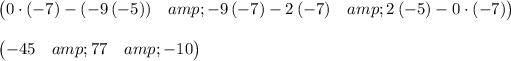

The area of the triangle is