Question

The kinetic energy of a rotating body is generally written as K=12Iω2, where I is the moment of inertia. Find the moment of inertia of the particle described in the problem introduction with respect to the axis about which it is rotating.

Answer 1

See explanation

Step-by-step explanation:

We have a mass
`m` revolving around an axis with an angular speed
`\omega`, the distance from the axis is
`r`. We are given:

`\omega = 10 [rad/s]\\r=0.5 [m]\\m=13[Kg]`

and also the formula which states that the kinetic rotational energy of a body is:

`K =(1)/(2)I\omega^2`.

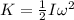Now we use the kinetic energy formula

`K =(1)/(2)mv^2`

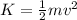
where
`v` is the tangential velocity of the particle. Tangential velocity is related to angular velocity by:

`v=\omega r`

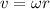
After replacing in the previous equation we get:

`K =(1)/(2)m(\omega r)^2`

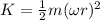
now we have the following:

`K =(1)/(2)m(\omega r)^2 =(1)/(2)Iw^2`

therefore:

`mr^2=I`

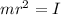
then the moment of inertia will be:

`I = 13*(0.5)^2=3.25 [Kg*m^2]`