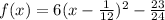Answer:
The equation in standard form is:
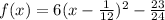
Explanation:
Given function:
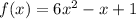
We need to convert this in standard form which is given by:
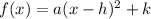
where
 represent co-efficient of leading term which is
represent co-efficient of leading term which is

and
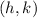 is the vertex (minimum and maximum point) of the curve.
is the vertex (minimum and maximum point) of the curve.
 can be found out using formula
can be found out using formula
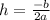
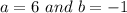
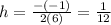
We can find
 by finding
by finding
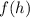 as
as
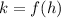 .
.
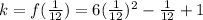
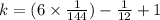
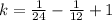
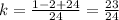
Thus the equation in standard form is: