Question

if you throw a rock straight up at a speed of 19m/s. How long goes it take the ball to reach its maximum height?

Answer 1

It requires 1.9 seconds to reach maximum height.

Step-by-step explanation:

As per given question,

Initial velocity (U) =19 m/s

Final velocity (V) = 0 m/s

`\text { Taking acceleration due to gravity }(a)=10 \mathrm{m} / \mathrm{s}^(2)`

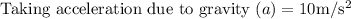
Maximum height = S

Time taken is "t"

Calculating time taken to reach maximum height:

We know that time taken to reach the maximum height is calculated by using the formula V = U + at

Substitute the given values in the above equation.

Final velocity is “0” as there is no velocity at the maximum height.

`0=19+10 * t`

`-19=10 * t`

`(-19)/(10)=t`

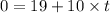
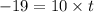
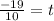
t = 1.9 seconds.

The time taken to reach maximum height is 1.9 seconds.

Calculating maximum height:

`\text { Consider the equation } V^(2)-U^(2)=2 a S`

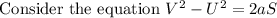
Solving the equation we will get the value of S

`0-19^(2)=2 *(-10) * \mathrm{S} .(-\text { is due to opposite of gravity) }`

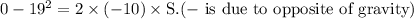
-361 = -20S

Negative sign cancel both the sides.

`\mathrm{S}=(361)/(20)`

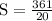
S = 18.05 m

Maximum height is 18.05 m .