Question

A 50 kg runner runs up a flight of stairs. The runner starts out covering 3 steps every second. At the end the runner stops. This slowing occurs at a constant rate. The end also occurs at a height of 30 steps. Each step has a height of 30 cm. a. How much mechanical work did the runner do over the 30 steps? b. What is the average total power output of the runner over the 30 steps?

Answer 1

To solve the problem it is necessary to take into account the concepts of kinematic equations of motion and the work done by a body.

In the case of work, we know that it is defined by,

`W = F * d`

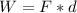
Where,

F= Force

d = Distance

The distance in this case is a composition between number of steps and the height. Then,

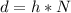`d=h*N`, for h as the height of each step and N number of steps.

On the other hand we have the speed changes, depending on the displacement and acceleration (omitting time)

`V_f^2-V_i^2 = 2a\Delta X`

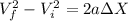
Where,

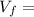`V_f =` Final velocity

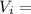`V_i =` Initial Velocity

a = Acceleration

`\Delta X =` Displacement

PART A) For the particular case of work we know then that,

`W = F*d`

`W = m*g*(h*N)`

`W = 50*9.8*(0.3*30)`

`W = 4.41kJ`

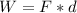
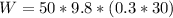
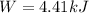
Therefore the Work to do that activity is 4.41kJ

PART B) To find the acceleration (from which we can later find the time) we start from the previously given equation,

`V_f^2-V_i^2 = 2a\Delta X`

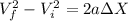
Here,

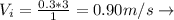`V_i = (0.3*3)/(1) = 0.90m/s\rightarrow`3 steps in one second

`v_f = 0`

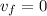
Replacing,

`V_f^2-V_i^2 = 2a\Delta X`

`0-0.9^2=2a(30*0.3)`

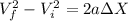
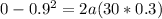
Re-arrange for a,

`a = -(0.9^2)/(2*30*0.3)`

`a = -45*10^(-3)m/s^2`

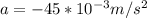
At this point we can calculate the time, which is,

`t = (\Delta V)/(a)`

`t = (0-0.9)/(-45*10^(-3))`

`t = 20s`

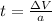
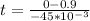
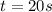
With time and work we can finally calculate the power

P = \frac{W}{t} = \frac{4.41}{20}

P = 0.2205kW