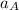Question

Satellite A orbits a planet at a distance d from the planet’s center with a centripetal acceleration a0. A second identical satellite B orbits the same planet at a distance 2d from the planet’s center with centripetal acceleration ab. What is the centripetal acceleration ab in terms of a0?

Answer 1

To solve this problem it is necessary to use the concepts related to the Gravitational Force and Newton's Second Law, as far as we know:

`F_g = (GMm)/(r^2)`

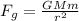
Where,

G = Gravitational constant

M = Mass of earth (in this case)

m = mass of satellite

r = radius

In the other hand we have the second's newton law:

`F = ma`

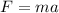
Where,

m = mass

a = acceleration

Equation both equations we have,

`ma = (GMm)/(r^2)`

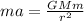
For the problem we have that,

Satellite A:

`ma_A = (GMm)/(r^2)`

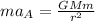
Satellite B:

`ma_B = (GMm)/((2r)^2)`

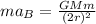
The ratio between the two satellites would be,

`(ma_A)/(ma_B)= ((GMm)/(r^2))/((GMm)/((2r)^2))`

Solving for a_B,

`a_B = (a_A)/(4)`

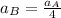
Therefore the centripetal acceleration of
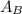`A_B` is a quarter of
`a_A`