Answer:
The time period on Titan is 2.67 hours.
Step-by-step explanation:
Given that,
Acceleration = 1.37 m/s²
Time on earth = 1 hour
Period of oscillation on earth

Where, L = length of the pendulum
The length of pendulum will be the same on the Titan.
The period of oscillation on Titan
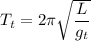
We need to calculate the time period on Titan


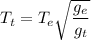
Put the value into the formula
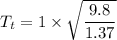
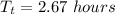
Hence, The time period on Titan is 2.67 hours.